What hyperparameters are
Episode 4 - The accuracy of a neural network depends also by its structure and not just by its weights and biases
Hyperparameters
The Gradient Descent algorithm—seen in the previous episode—aims to find the optimal value for each weight and bias inside the neural network in order to provide a good model in terms of accuracy. However, this method alone is not enough to guarantee a strong and reliable neural network. In fact, the accuracy also depends on many other factors that can’t always be optimized through a function; these factors are also called Hyperparameters.
These kinds of variables, which are set before training, are responsible for the amount of time the neural network takes to be trained, and they can be divided into two different classes.
Model hyperparameters
The number of layers
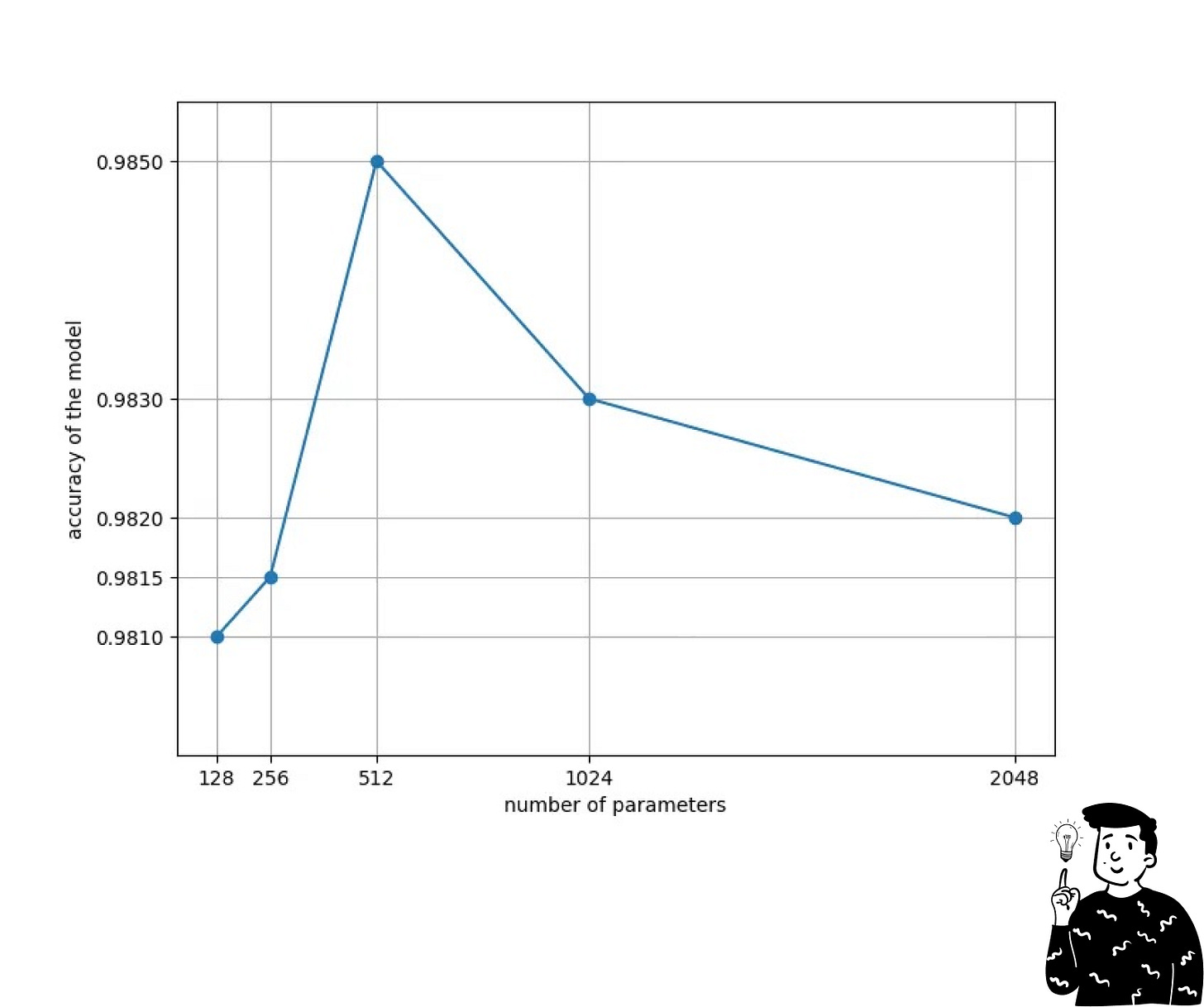
These are all the variables that define the structure of the neural network. For example, the number of layers and the number of nodes that we want to use belong to this class. Obviously, increasing the number of layers will increase the time—and computational power—required to train the model. On the other hand, this might help the network to find more hidden patterns (maybe also thanks to CNNs, which I will discuss in more detail in the next episodes).
Having too many layers can be a disadvantage because it is not guaranteed that the model with more layers is the one that works best. In fact, there is a cutoff point where the model starts to drop in terms of accuracy.
This issue is commonly caused by the model being more exposed to overfitting problems with more nodes. To tackle this, there is another hyperparameter that can be set: Dropout (discussed below under the class of algorithm hyperparameters).
Activation function
Besides the choice of the number of layers and nodes, there is the activation function—I’ve already talked in depth about them in episode #2 (learn more). These are a set of non-linear functions that are applied at each node to expand the information that the neural network can capture. Some examples are:
The Sigmoid function—in case the model is making a binary classification
The Softmax function—for multi-class predictions
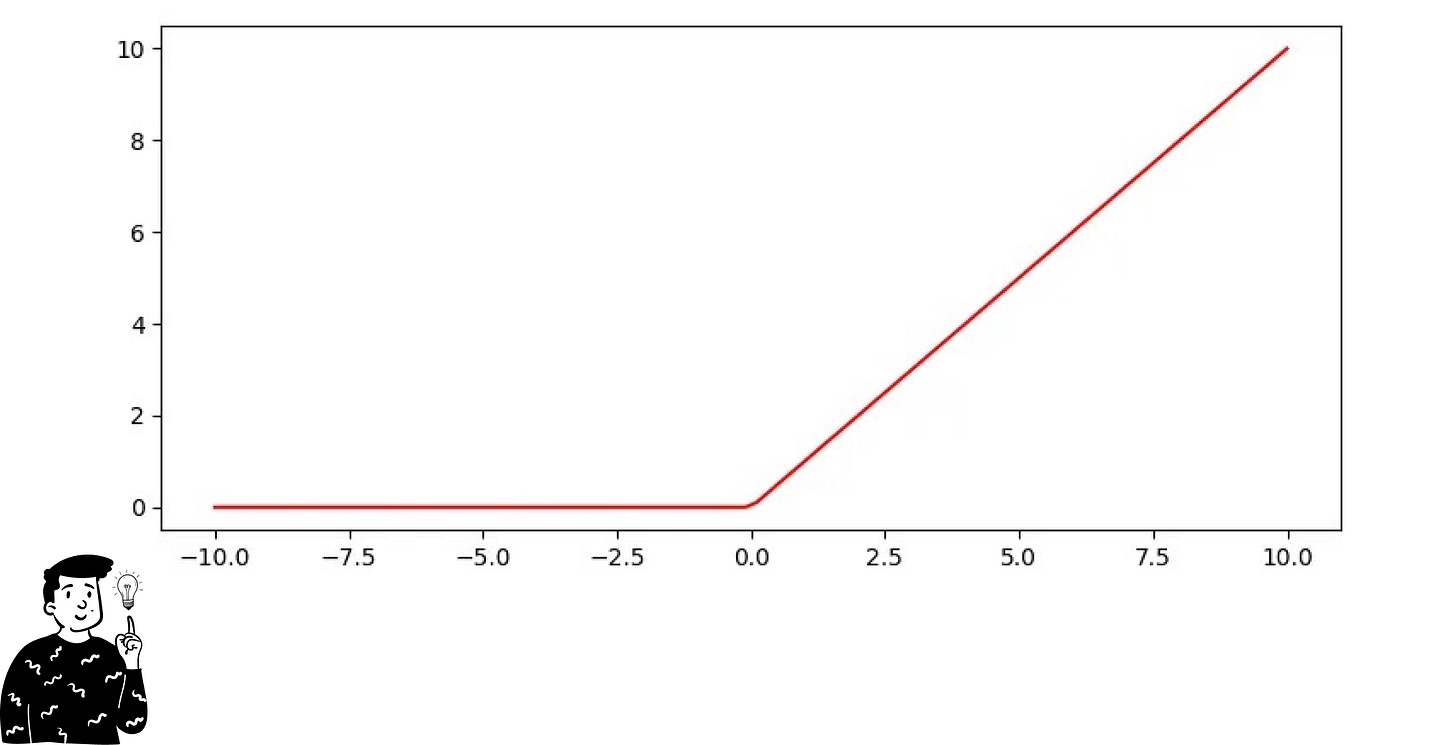
The ReLu function—the most popular for general purposes
Algorithm hyperparameters
Dropout
This process works by randomly dropping out a fraction of neurons during the training phase of the neural network. This is done because neurons work to identify patterns in the data, and sometimes certain neurons become overly reliant on the outputs of other specific neurons (a process also known as co-adaptation). They tend to become too specific, thus leading to overfitting of the model.
The number of nodes dropped out at each iteration in the training process is determined by a hyperparameter that indicates the probability of a dropout (commonly referred to with the letter p). Usually, the most common values of p are between 0.2 and 0.5, and this technique is used in larger networks instead of smaller ones.
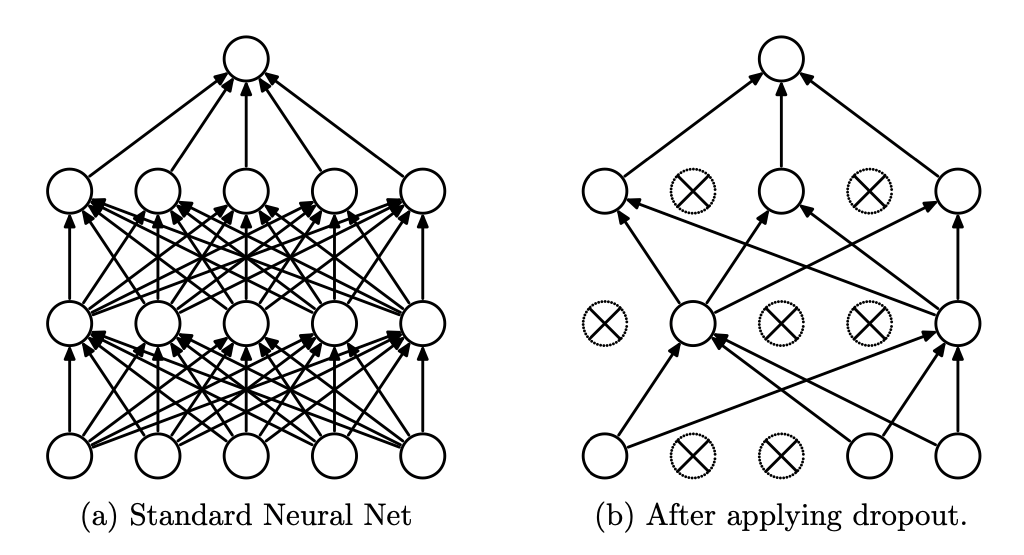
If you’re interested to learn more about the dropout technique I suggest to read this paper made in 2014.
Learning rate
This kind of parameter depends on the optimization algorithm we use. Indeed, as discussed last time, Gradient Descent is an iterative function that aims to minimize a cost function by moving toward the minimum, and the velocity is set by the learning rate. The higher the learning rate, the bigger the step that the algorithm makes at each iteration.
At first glance, it might seem better to assign a large value to move toward the minimum faster, but this increases the risk of overshooting, and the algorithm could start to oscillate around the local minimum. In practice, the learning rate is updated at each iteration and depends on two parameters:
Decay: The gradual reduction of the learning rate at each iteration to be more precise near the minimum point.
Momentum: Used to prevent oscillations and helps to remember the direction taken by the vector in the previous step. This means that if the gradient keeps pointing in the same direction, the momentum will continue to push the updates in that direction.
Optimizer
The optimizer chosen is also considered a hyperparameter. Besides Gradient Descent, there are other kinds of optimizers that can perform better in different situations:
Adam: Used with deep learning models that have a complex architecture (CNNs, RNNs, GPT). Its advantage is that the learning rate is automatically adjusted during training.
RMSprop: Commonly used for time series forecasting and with neural networks that use LSTM; it is quite similar to the Adam optimizer.
Other kinds of algorithm hyperparameters
There are plenty of other hyperparameters that can be tuned; some of them are:
The Number of Epochs: This is the number of times the training data is passed through the network.
The Batch Size: This represents the number of training examples used to train the model at each iteration.
Loss Function: As seen in previous episodes, this is an objective function used to evaluate the performance of the model.
Conclusion
As we’ve seen today, building a neural network doesn’t just depend on finding the best values for weights and biases; there are plenty of different things you have to keep in mind while building your model. In the next episode, we’ll talk about the backpropagation, the way Neural Networks learn from errors.
(Probably if you click on my account you can already see the next episode)